Перейти к:
Обоснование новой методики при бесконтактных измерениях в электроразведке методом сопротивлений
https://doi.org/10.32454/0016-7762-2023-65-4-27-36
Аннотация
Введение. Методы сопротивлений — это электрическое зондирование и электропрофилирование с различными установками. Первоначально измерения проводили на постоянном токе, а затем на низкочастотном переменном токе. В случае постоянного тока единственные источники первичного электрического поля в этих методах — заряды токовых электродов A, B, а измеряемая величина — равное разности потенциалов ΔUMN напряжение электрического поля E в линии MN с измерительными электродами M, N. По результатам измерений определяют (удобное для интерпретации результатов измерений) кажущееся удельное электрическое сопротивление ρк. Однако в ряде случаев, например при проведении измерений в районах многолетнемерзлых пород, бывает сложно обеспечить надежное заземление электродов. Поэтому полвека назад были начаты исследования с целью обоснования возможности бесконтактных измерений в методе электропрофилирования на переменном токе I в линии AB. До последнего времени методика бесконтактных изменений и интерпретации получаемых результатов опиралась на приближенные подходы, а не на «строгое» решение прямой задачи электродинамики. Цель. Объективное обоснование методики бесконтактных измерений на основе решения прямой задачи электродинамики.
Материалы и методы. Метод исследования — математическое моделирование и анализ полученных результатов.
Результаты. Приведены результаты расчетов для модели, соответствующей возможным условиям при бесконтактных измерениях в электроразведке методом сопротивлений. Рассмотрен случай, когда генераторная линия AB гармонически меняющегося тока I расположена в воздухе, на высоте h над однородным проводящим полупространством с удельным электрическим сопротивлением ρ2.
Заключение. По сравнению с применяемой сейчас при бесконтактных измерениях методикой более эффективным для нахождения ρ2 является определение кажущегося удельного электрического сопротивления по меняющейся синфазно с током I в генераторной линии AB реактивной составляющей напряжения электрического поля E в измерительной линии MN.
Ключевые слова
Для цитирования:
Каринский А.Д., Иванов А.А., Зуденков И.А., Матюшенко А.А., Новиков П.В. Обоснование новой методики при бесконтактных измерениях в электроразведке методом сопротивлений. Proceedings of Higher Educational Establishments: Geology and Exploration. 2023;(4):27-36. https://doi.org/10.32454/0016-7762-2023-65-4-27-36
For citation:
Karinskiy A.D., Ivanov A.A., Zudenkov I.A., Matyushenko A.A., Novikov Р.V. Substantiation for a new non-contact measurement technique in electrical resistance surveys. Proceedings of higher educational establishments. Geology and Exploration. 2023;(4):27-36. (In Russ.) https://doi.org/10.32454/0016-7762-2023-65-4-27-36
В семидесятых годах двадцатого века были начаты исследования с целью обоснования возможности применения бесконтактных измерений в электроразведке методом сопротивлений. Необходимость применения такой модификации возникает в различных ситуациях. Например, при проведении измерений методами сопротивлений в зонах скальных или многолетнемерзлых пород при наличии снежного покрова либо практически непроводящих искусственных покрытий. Кроме того, отсутствие необходимости заземления токовых (A, B) и измерительных (M, N) электродов позволяет многократно ускорить процесс измерений. Некоторые результаты таких исследований были опубликованы, например, в работах [2][3][12—16]. Однако теоретическое обоснование проведения бесконтактных измерений и интерпретации получаемых результатов в этих работах основывалось не на «строгом» решении соответствующей прямой задачи электродинамики, а на приближенных подходах. Причина этого, по-видимому, связана с тем, что некоторые трудности у авторов этих работ возникали при получении «строгого» решения соответствующей прямой задачи электродинамики и проведении на основе этого решения математического моделирования.
Очевидно, что проведение бесконтактных измерений в методах сопротивлений возможно лишь при переменном токе I в питающей линии AB. В случае постоянного тока I таким измерениям препятствует явление электростатической индукции. Некоторые результаты математического моделирования для электроразведки методами сопротивлений при переменном токе I = I0cos (2πft) = I0cos (ωt) приведены в статье [7]. Здесь I0 — амплитуда тока, f — частота, t — время, ω — круговая частота. В этой статье были приведены решение прямой задачи электродинамики и полученные на его основе результаты математического моделирования для случая, когда линия AB переменного тока лежит на поверхности «двухслойного» проводящего полупространства. Основой для получения решения задачи послужила методика, описанная в книге [5]. Эта же методика была применена нами при получении приведенных ниже результатов математического моделирования. Ранее результаты исследований по этой тематике были представлены на конференциях [8—11]. Был также получен патент [6].
Приведенные ниже результаты численных расчетов получены при частоте f = 16 кГц. Это та рабочая частота, которая была выбрана для нескольких видов аппаратуры при бесконтактных измерениях в методах сопротивлений.
Модель и алгоритм
На рисунке 1 показана модель, для которой было получено решение прямой задачи электродинамики и проведены численные расчеты.
Горизонтальная плоскость S разделяет полупространства V1 (воздух) и V2 (приповерхностные горные породы). Генераторная (AB) и измерительная (MN) линии расположены в верхнем полупространстве на одной прямой, параллельной оси X, на высоте h над границей S. Решение соответствующей прямой задачи электродинамики приведено в электронной версии учебника [1]. При применении комплексной записи напряжение EMN электрического поля E в измерительной линии MN определяет двойной интеграл (формула 1):
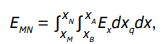 (1)
(1)
где xB ≤ xq ≤ xA, xM ≤ x ≤ xN (см. рис. 1).
Подынтегральная функция в формуле (1) — скалярная компонента Ex электрического поля E:
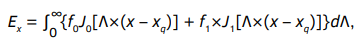 (2)
(2)
которую определяет несобственный интеграл в смысле главного значения. В выражении (2) J0[Λ×(x – xq)], J1[Λ×(x – xq)] — функции Бесселя первого рода нулевого и первого порядка аргумента Λ×(x – xq), а множители f0 и f1 зависят от параметров показанной на рисунке 1 модели, от частоты f и от переменной интегрирования Λ. Для численного расчета несобственного интеграла в смысле главного значения в правой части формулы (2) мы пользовались преобразованием Эйлера. Применение этого преобразования описано в работе [4].
Приведенные на рисунках 2—4 результаты математического моделирования получены для предельной дипольной осевой установки (AB→0, MN→0). Для такой установки напряжение EMN пропорционально определяемой выражением (2) компоненте Ex поля E в центре отрезка MN. Значения кажущегося удельного электрического сопротивления ρк для такой установки определены двумя способами. Значения ρк(Ex) для предельной дипольно-осевой установки определены традиционным способом по формуле: ρк(Ex) = K×|Ex|/I0, где |Ex| — амплитуда компоненты Ex, K = π×x3 — коэффициент предельной дипольной осевой установки, расположенной на поверхности проводящего полупространства, а x — расстояние между центрами генераторного и измерительного диполей. Значения ρк(|Re Ex|) определены по амплитуде |Re Ex| реактивной составляющей Re Ex компоненты Ex меняющейся синфазно либо в противофазе с током I в генераторном диполе AB. То есть ρк(|Re Ex|) = K×|Re Ex|/I0.
Результаты расчетов на рисунках 6 получены для приближающихся к реальным условиям при электроразведочных измерениях конечных расстояний между всеми электродами. Значения кажущегося удельного электрического сопротивления ρк на рисунке 6 определены двумя способами. При применяемом в настоящее время при бесконтактных измерениях подходе ρк(EMN) = K×|EMN |/I0, где |EMN | — амплитуда напряжения электрического поля в линии MN, 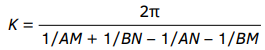 — коэффициент электроразведочной установки. При предлагаемом нами способе кажущееся удельное электрическое сопротивление ρк(Re EMN) = K×|Re EMN |/I0, где |Re EMN | — амплитуда реактивной составляющей напряжения EMN электрического поля E в линии MN, меняющейся синфазно с током I в генераторной линии AB.
— коэффициент электроразведочной установки. При предлагаемом нами способе кажущееся удельное электрическое сопротивление ρк(Re EMN) = K×|Re EMN |/I0, где |Re EMN | — амплитуда реактивной составляющей напряжения EMN электрического поля E в линии MN, меняющейся синфазно с током I в генераторной линии AB.
Результаты моделирования
На рисунке 2 представлены зависимости ρк(Ex) от разноса x. При расчетах в полупространстве V2 была задана диэлектрическая проницаемость ε2 = 10. Хотя легко оценить, что при частоте 16 кГц и значениях ρ2 менее первых десятков тысяч Ом×м выбор величины ε2 несущественен, так как при любых, реальных для горных пород значениях ε2 и при ρ2 < 10 000 Ом×м можно пренебречь влиянием на электромагнитное поле токов смещения в нижнем полупространстве.
Результаты моделирования, представленные на рисунке 2, показали, например, что при высоте h = 5 см величина ρк ≈ ρ2, если разнос x ≈ 15 м, а при h = 10 см величина ρк ≈ ρ2, если разнос x ≈ 20 м. При h = 20 см значения ρк значительно больше ρ2 при любых разносах x. Если x > 25—30 м, то значения ρк перестают зависеть от h (индукционная асимптота).
На рисунке 3 показаны зависимости ρк(Ex) от разноса x при фиксированных высотах h = 5 см (а) и h = 10 см (б) и при трех значениях удельного электрического сопротивления ρ2. Из приведенных на этом рисунке результатов моделирования следует, что при частоте f = 16 кГц, указанных выше высотах h и разносах x порядка 10 и 20 метров величина ρк ≈ ρ2 только при высоких значениях ρ2 (порядка 1000 Ом×м, как на рисунке 3 и выше).
Значения ρк(|Re Ex|) на рисунке 4 определены по амплитуде |Re Ex|, составляющей Re Ex, меняющейся синфазно либо в противофазе, с током I в генераторном диполе AB. То есть ρк(|Re Ex|) = K×|Re Ex|/I0. Некоторые особенности графиков на этом рисунке связаны с тем, что функция Re Ex(x) не является знакопостоянной. Результаты расчетов, представленные на рисунке 4а, получены при высоте h = 5 см, а на рисунке 4б — при h = 10 см.
При сравнении рисунка 4 с рисунками 2 и 3 видно, что определение по значению |Re Ex| кажущегося удельного электрического сопротивления ρк при невысоких значениях ρ2 может иметь безусловные преимущества по сравнению с применяемым сейчас определением ρк по величине |Ex|. В соответствии с результатами расчетов на рисунке 4 при заданной частоте f можно выбрать такой разнос x, чтобы при широких пределах изменения удельного электрического сопротивления ρ2 значения ρк(|Re Ex|) были близки к ρ2, В пределах изменения ρ2 от 10 до 1000 Ом×м таким оптимальным является разнос x ≈ 8—10 м.
Таким образом, приведенные выше результаты численных расчетов показали, что при наиболее типичных для немерзлых осадочных горных пород удельных электрических сопротивлениях в случае бесконтактных измерений вместо амплитуды напряжения в линии MN целесообразно измерять реактивную составляющую этого напряжения, меняющуюся синфазно с током I в линии AB. Попробуем теперь дать этому физическое истолкование.
Пусть горизонтальный переменный электрический диполь AB с центром в начале декартовых координат расположен в воздухе на высоте h над плоской горизонтальной границей S однородного проводящего немагнитного полупространства с удельным электрическим сопротивлением ρ2. В этом случае электрическое поле с напряженностью E создают следующие четыре возбудителя: 1) электрические заряды на концах отрезка AB, величины которых не зависит от ρ2; 2) индукционное поле E, возбуждаемое первичным магнитным полем отрезка AB тока I. Это поле вообще не зависит от параметров среды; 3) индукционное поле E, возбуждаемое объемными токами проводимости и токами смещения. В ближней зоне такая составляющая поля переменного электрического диполя не зависит от электрических параметров среды (см. [1]); 4) Кулоново (гальваническое) поле E, создаваемое поверхностными зарядами с поверхностной плотностью σ, индуцированными на границе S, которое зависит от коэффициента контрастности границы S, и, следовательно, именно эта составляющая поля E зависит от удельного электрического сопротивления ρ2 проводящего полупространства.
Если ось Z направлена по нормали к плоскости S, то поверхностная плотность зарядов σ = ε0×ΔEz, где ε0 — электрическая постоянная, а ΔEz — разрыв на этой плоскости нормальной к Sz компоненты электрического поля E. Сразу отметим, что в случае гармонически меняющегося поля плотность σ имеет две составляющие: реактивную Re σ, меняющуюся синфазно либо в противофазе с током I, и активную Im σ, отличающуюся по фазе от тока I на ±π/2 радиан. Заряды с этими плотностями — источники, соответственно, реактивной и активной составляющих поля E.
На рисунке 5 показаны примеры того, как могут быть распределены плотности зарядов Re σ и Im σ на участке плоскости S при высоте h = 20 см и двух разных значениях ρ2. На верхних рисунках (а, б) ρ2 = 10 Ом×м, а на нижних рисунках (в, г) ρ2 = 10 000 Ом×м. Слева, на рисунках а, в, показаны карты Re σ, а справа, на рисунках б, г — карты Im σ.
При сравнении рисунков а, в видим, что распределение на плоскости S составляющей Re σ, а следовательно, и создаваемое этими зарядами поле Re E существенно зависит от величины ρ2. Значения Im σ на рисунках б, г по абсолютной величине примерно на два порядка выше абсолютных величин |Re σ|, но карты Im σ на этих рисунках практически одинаковы. То есть интересующий нас (искомый) параметр ρ2 почти не влияет на плотность Im σ и на создаваемое этими зарядами поле Im E, а также на суммарное поле E. Удельное электрическое сопротивление ρ2 влияет на плотность Re σ и, следовательно, на поле Re E.
Графики на рисунках 2—4 и карты на рисунке 5 получены при разносе AB→0. Ниже будут представлены результаты математического моделирования для дипольной осевой установки (ДОУ) для приближающихся к реальным условиям при электроразведочных измерениях конечных расстояниях между всеми электродами.
На рисунке 6 при нескольких значениях ρ2 представлены зависимости кажущегося удельного электрического сопротивления ρк от высоты h для установки B2A6M2N. То есть расстояния между (точечными) электродами B и A, а также между электродами M и N равны 2 метрам, а расстояние между электродами A и M равно 6 метрам (см. рис. 1). Сплошными линиями показаны зависимости ρк(EMN) от h, где EMN — амплитуда напряжения поля E в линии MN. Видим, что эти значения в той или иной степени позволяют оценить истинное удельное электрическое сопротивление ρ2 проводящего полупространства только при высотах h, равных первым единицам сантиметров, особенно при невысоких значениях ρ2. При тех пределах изменения ρ2, при которых выполнены расчеты, и при высотах h более 8 сантиметров значения ρк(EMN) практически не зависят от ρ2.
Штрихпунктирными линиями показаны зависимости ρк(Re EMN) от h. Из полученных результатов численных расчетов следует, что даже при высотах h в десятки сантиметров величины ρк(Re EMN) испытывают значительное влияние ρ2.
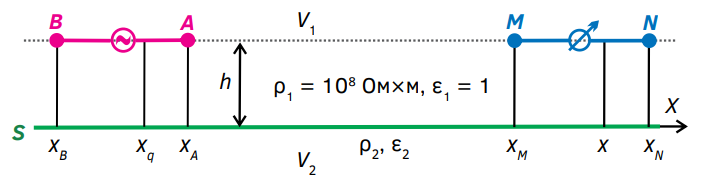
Рис. 1. Модель среды и электроразведочной установки
Fig. 1. Geoelectrical model and electrical array
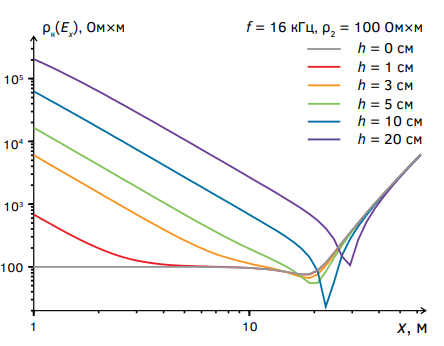
Рис. 2. Зависимости ρк(Ex) от разноса x при нескольких значениях высоты h
Fig. 2. Dependences of ρк(Ex) on the spacing of x for several values of height h
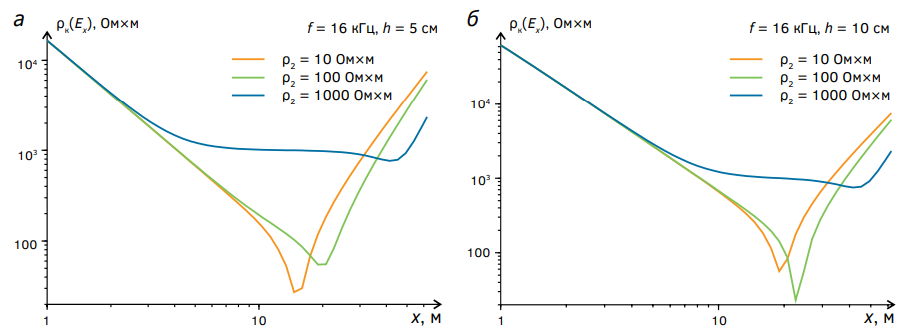
Рис. 3. Зависимости ρк(Ex) от разноса x при нескольких значениях ρ2
Fig. 3. Dependences of ρк(Ex) on the spacing of x for several values of ρ2
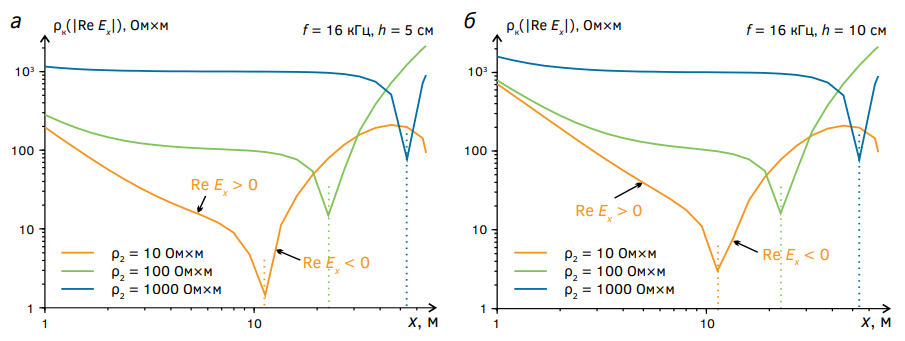
Рис. 4. Зависимости ρк(Re Ex) от разноса x при нескольких значениях ρ2
Fig. 4. Dependences of ρк(Re Ex) on the spacing of x for several values of ρ2
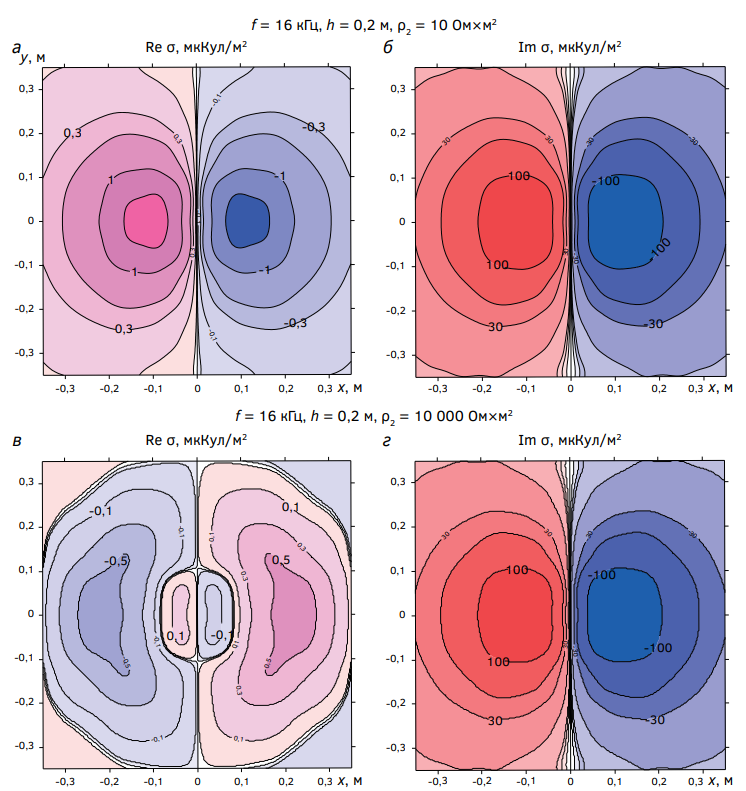
Рис. 5. Распределение плотностей зарядов Re s и Im s на плоскости S
Fig. 5. Distribution of charge densities Re s and Im s on the S plane
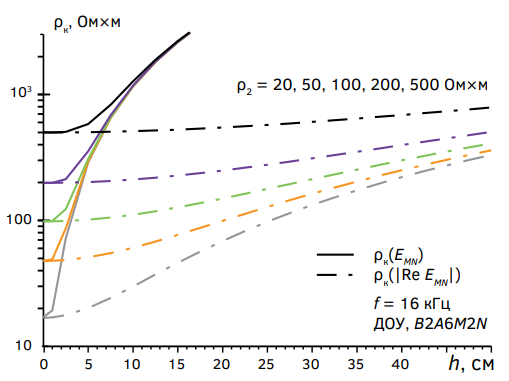
Рис. 6. Зависимости ρк(EMN) и ρк(Re EMN) от высоты h при нескольких значениях ρ2
Fig. 6. Dependencies ρк(EMN) and ρк(Re EMN) from the height h at several values ρ2
Заключение
Очевидно, что определение ρк по реактивной составляющей Re EMN напряжения EMN может позволить значительно расширить область применения бесконтактной модификации электроразведки методом сопротивлений.
По рассмотренной в этой работе проблематике дальнейшие исследования, по нашему мнению, следует провести по следующим направлениям:
1) Получение в аналитическом виде решения соответствующей прямой задачи электродинамики для модели среды с двумя плоскопараллельными границами. Составление соответствующих такой модели программ для компьютера и проведение численных расчетов;
2) Проведение физического моделирования с соблюдением принципов геометрического и электродинамического подобия с измерением реактивной компоненты Re EMN;
3) Создание габаритного макета аппаратуры позволяющего измерять Re EMN и проведение измерений с этим макетом.
Полученные авторами результаты математического моделирования могут послужить основой при конструировании серийной аппаратуры для бесконтактных измерений в методе электропрофилирования, обоснования методики измерений и интерпретации результатов измерений.
Список литературы
1. Альпин Л. М., Даев Д.С., Каринский А.Д. Теория полей, применяемых в разведочной геофизике. Учебник для ВУЗов. Часть IV. М.: МГРИ, 2020. 104 с.
2. Груздев А.И. Сравнение различных методик контактных и бесконтактных измерений в условиях средней полосы России // Инженерные изыскания. 2014. Т. 7. №9/10. С. 32—37.
3. Груздев А.И., Бобачев А.А., Шевнин В.А. Определение области применения бесконтактной технологии метода сопротивлений // Вестник Московского университета. Серия 4: Геология. 2020. Т. 5. № 5, С. 100—106.
4. Дашевский Ю.А. Применение преобразования Эйлера для расчета стационарных и гармонических электромагнитных полей в горизонтальнослоистых средах. Электромагнитные методы геофизических исследований. / Под ред. Ю.Н. Антонова. Новосибирск, 1982. С. 78—88.
5. Заборовский А.И. Переменные электромагнитные поля в электроразведке. М.: Изд-во МГУ, 1960. 186 с.
6. Иванов А.А, Каринский А.Д. Способ бесконтактной электроразведки. Патент России № 2785037. 16.12.2022. Бюл. № 35.
7. Каринский А.Д., Шевнин В.А. Влияние индукции на результаты ВЭЗ на переменном токе. // Геофизика. 2001. Т. 9. № 5. С. 50—56.
8. Каринский А.Д., Кудина Я.О., Матюшенко А.А. К бесконтактной модификации электроразведки методом сопротивлений // Разведочная геофизика и геоинформатика: мат-лы Всеросс. науч.-практич. конф. М.: Российский государственный геологоразведочный университет им. С. Орджоникидзе, 2021. С. 28—33.
9. Каринский А.Д., Кудина Я.О., Матюшенко А.А. Бесконтактные измерения в электроразведке методом сопротивлений; опыт математического моделирования // Новые идеи в науках о Земле: мат-лы XV Междунар. науч.-практич. конф. Т. IV. М.: Российский государственный геологоразведочный университет им. С. Орджоникидзе, 2021. С. 298— 302.
10. Каринский А.Д., Шевнин В.А., Иванов А.А. Бесконтактные измерения в электроразведке методом сопротивлений; опыт математического моделирования // Мат-лы VIII Всеросс. школы-семинара по электромагнитным зондированиям Земли им. М.Н. Бердичевского и Л.Л. Ваньяна. М.: Институт физики Земли им. О.Ю. Шмидта РАН, 2021. С. 279—283.
11. Каринский А.Д., Кудина Я.О., Матюшенко А.А. К обоснованию методики бесконтактных измерений в электроразведке методом сопротивлений // Разведочная геофизика и геоинформатика: мат-лы Всеросс. науч.-практич. конф. М.: Российский государственный геологоразведочный университет им. С. Орджоникидзе, 2022. С. 9—12.
12. Нахабцев А.С., Сапожников Б.Г., Яблучанский А.И. Электропрофилирование с незаземленными рабочими линиями. Л.: Недра. 1985. 96 с.
13. Тимофеев В.М., Бяшков Г.П. О некоторых путях повышения эффективности электропрофилирования при инженерно-геокриологической съемке // Тр. ВСЕГИНГЕО. 1976. Т. 1. № 81. С. 28—36.
14. Calvert H.T. Capacitive-coupled resistivity survey of ice-bearing sediments, Mackenzie Delta // SEG technical program expanded abstracts. 2002. V. 1. No. 1. P. 696—698.
15. Grard R., Tabbagh A. A mobile four-electrode array and its application to the electrical survey of planetary grounds at shallow depths // J. Geophys. Res. 1991. V. 96. No. B3. P. 4117—4123.
16. Kuras O., Beamish D., Meldrum P.I., Ogilvi R.D. Fundamentals of the capacitive resistivity technique // Geophysics. 2006. V. 71. No. 3. P. G135— G152.
Об авторах
А. Д. КаринскийРоссия
Каринский Александр Дмитриевич — доктор физико-математических наук, профессор кафедры геофизики
23, Миклухо-Маклая улица, Москва 117997
А. А. Иванов
Россия
Иванов Андрей Александрович — кандидат геолого-минералогических наук, доцент кафедры геофизики
23, Миклухо-Маклая улица, Москва 117997
И. А. Зуденков
Россия
Зуденков Иван Андреевич — аспирант кафедры геофизики
23, Миклухо-Маклая улица, Москва 117997
А. А. Матюшенко
Россия
Матюшенко Анна Алексеевна — аспирант кафедры математики
23, Миклухо-Маклая ул., г. Москва 117997
П. В. Новиков
Россия
Новиков Петр Вячеславович — кандидат технических наук, доцент кафедры геофизики
23, Миклухо-Маклая улица, Москва 117997
Рецензия
Для цитирования:
Каринский А.Д., Иванов А.А., Зуденков И.А., Матюшенко А.А., Новиков П.В. Обоснование новой методики при бесконтактных измерениях в электроразведке методом сопротивлений. Proceedings of Higher Educational Establishments: Geology and Exploration. 2023;(4):27-36. https://doi.org/10.32454/0016-7762-2023-65-4-27-36
For citation:
Karinskiy A.D., Ivanov A.A., Zudenkov I.A., Matyushenko A.A., Novikov Р.V. Substantiation for a new non-contact measurement technique in electrical resistance surveys. Proceedings of higher educational establishments. Geology and Exploration. 2023;(4):27-36. (In Russ.) https://doi.org/10.32454/0016-7762-2023-65-4-27-36









































