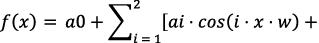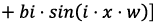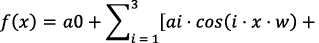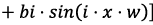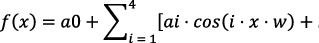Перейти к:
Построение и анализ некоторых математических моделей, связанных с временными вариациями гравитационного поля
https://doi.org/10.32454/0016-7762-2025-67-2-76-94
EDN: JSULIZ
Аннотация
Введение. Изучение временных вариаций гравитационного поля Земли представляет собой актуальную задачу современной геофизики, особенно в контексте анализа влияния внешних и внутренних факторов на силу тяжести. Традиционные подходы к моделированию гравитационного поля основаны на теоретически заданных предпосылках, что ограничивает их применимость в условиях высокой вариативности геодинамических процессов.
Цель. Разработка и апробация инновационного подхода к построению математических моделей временных изменений гравитационного поля, не опирающегося на заранее заданные теоретические модели, а базирующегося на эмпирических данных и феноменологическом описании случайных процессов.
Материалы и методы. Экспериментальная часть исследования была реализована на фундаментальном гравиметрическом пункте «Ледово» с использованием группы гравиметров различных типов. Проведены инструментальные измерения вариаций силы тяжести. Для анализа полученных данных использовались спектрально-статистические методы и преобразование Фурье. Особое внимание уделено сравнению показателей, зарегистрированных различными приборами. Дополнительно применялась процедура оптимального линейного сглаживания (ПОЛС) для построения обобщенной модели гравитационных вариаций.
Результаты. Анализ показал высокую степень согласованности измерений: коэффициент корреляции между гравиметрами ГНУ-КВ и CG-6 превысил 0,9, что подтверждает идентичность их спектральных характеристик и надежность данных. При этом установлено, что однозначное математическое описание вариаций затруднено из-за влияния слабоизученных геодинамических и случайных факторов. Построенная модель, основанная на ПОЛС, позволяет совместить элементы известных теоретических построений с учетом влияния «гостевых» процессов — внешних и локальных факторов неясной природы.
Заключение. Предложенный безмодельный подход и использование процедуры оптимального линейного сглаживания открывают новые возможности для более точного и гибкого описания временных вариаций гравитационного поля Земли. Разработанный методический подход может быть полезен при дальнейшем изучении геофизических процессов и развитии методов мониторинга изменений гравитационного поля.
Ключевые слова
Для цитирования:
Нигматуллин Р.Р., Белов А.П., Ерохин А.М., Мухаметзянов А.Р., Конешов В.Н., Дробышев М.Н. Построение и анализ некоторых математических моделей, связанных с временными вариациями гравитационного поля. Proceedings of Higher Educational Establishments: Geology and Exploration. 2025;67(2):76-94. https://doi.org/10.32454/0016-7762-2025-67-2-76-94. EDN: JSULIZ
For citation:
Nigmatullin R.R., Belov A.P., Erokhin A.M., Mukhametzyanov A.R., Koneshov V.N., Drobyshev M.N. Construction and analysis of mathematical models describing temporal variations of earth’s gravity field. Proceedings of higher educational establishments. Geology and Exploration. 2025;67(2):76-94. (In Russ.) https://doi.org/10.32454/0016-7762-2025-67-2-76-94. EDN: JSULIZ
1. Введение и постановка задачи
Колебания, постоянно регистрируемые на поверхности земной коры, являются результатом как природных, так и техногенных процессов. В последние годы наблюдается возросший интерес к изучению длинноволновых компонентов потенциальных полей, в частности к исследованию временных вариаций силы тяжести. Это связано с тем, что с изменением климата наблюдается не только увеличение уровня Мирового океана, но и локальные деформации на поверхности Земли, что приводит к изменению силы тяжести. Периодические изменения значений силы тяжести можно заранее вычислить путем использования различных способов [11][13][14]. Для изучения изменения силы тяжести из-за регионального поднятия в Фенноскандии [17] в течение более пяти лет применялся комплекс геофизических и геодезических методов. В него входили наряду со спутниковой информацией, непрерывной информацией GPS-наблюдений, данных приливных станций информация об абсолютных измерениях более чем в 30 пунктах Скандинавии. Были созданы соответствующие методики для сравнения результатов разных методов наблюдения. В результате была оценена точность работы каждого метода и доказано локальное поднятие земной поверхности этого региона. Оценка взаимосвязи гравиметрических измерений с геодезическими изменениями проводилась и в нашей стране [8]. Инструментальные измерения колебаний силы тяжести, полученные относительными гравиметрами, также предоставляют ценные данные для решения ряда фундаментальных и прикладных задач в геофизике, включая мониторинг землетрясений, вулканической активности и изменения распределения масс внутри Земли [12].
Надежные гравиметрические, сейсмометрические, метеорологические и прочие сопутствующие измерения являются необходимой основой, способствующей разработке динамических моделей и улучшению прогностических методов [1][2].
Целью данной работы является разработка и применение математических моделей для описания временных вариаций гравитационного поля Земли, а также оценка эффективности предложенного подхода на основе экспериментальных данных. Для достижения этой цели в работе решаются следующие задачи:
- Проведение инструментальных измерений колебаний силы тяжести с использованием группы гравиметров различных типов.
- Обработка и анализ полученных данных с применением спектрально-статистических методов и преобразования Фурье.
- Оценка корреляции между измерениями различных гравиметров для подтверждения их идентичности и надежности.
- Разработка общей модели вариаций гравитационного поля, основанного на инструментальных гравиметрических измерениях, учитывающей влияние случайных «гостевых» процессов.
Структура работы включает описание проведенного эксперимента и методов обработки данных [4], анализ полученных результатов, построение и оценку математических моделей, а также выводы и рекомендации для дальнейших исследований. Полученные результаты демонстрируют высокую корреляцию между гравиметрами ГНУ-КВ и CG-6, подтверждая идентичность их спектральных характеристик и надежность в регистрации вариаций гравитационного поля. Однако анализ также выявил сложности однозначного математического описания вариаций силы тяжести из-за влияния неучтенных случайных факторов, что подчеркивает необходимость дальнейших исследований и разработки более сложных комплексных моделей.
2. Описание экспериментов и обработка данных
2.1. Гравиметрический пункт
Исследования проводились параллельно с постоянно действующим комплексом геофизической аппаратуры, установленным Институтом физики Земли им. О.Ю. Шмидта Российской академии наук (ИФЗ РАН) на постаменте Фундаментального гравиметрического пункта «Ледово». Данный пункт находится в помещении гравиметрической лаборатории корпуса экспедиционной базы ИФЗ РАН, расположенном в 300 метрах от Щелковского шоссе. Постамент Фундаментального гравиметрического пункта «Ледово» представляет собой бетонный параллелепипед с размерами 7,3 м в длину, 1,1 м в ширину и около 4 м в глубину. Постамент не соприкасается с полом помещения, что минимизирует влияние вибраций и других механических помех на измерения.
2.2. Используемые приборы
В комплексе геофизической аппаратуры используются гравиметрические приборы различных типов, действующие на одних и тех же физических принципах и обладающие общим частотным диапазоном. Расположение всех гравиметров на одном геофизическом постаменте позволяет считать зарегистрированные инерционные помехи идентичными по происхождению [1][2]. Несмотря на это, различные типы гравиметров отличаются конструктивными особенностями упругих систем, что влияет на их точностные характеристики [6]. Давление, температура, дрейф нуля при данных измерениях не оказывают значительного влияния на результаты измерений.
При проведении эксперимента использовались следующие гравиметры:
- CG-6 Autograv: автоматизированный относительный гравиметр последней серии компании Scintrex, отличающийся высокой точностью и надежностью;
- CG-5 Autograv (CG-350, CG-351): автоматизированные относительные гравиметры, зарекомендовавшие себя как исключительно надежные приборы за десятилетие эксплуатации;
- ГНУ-КВ: кварцевый гравиметр, широко используемый для гравиразведочных работ в Советском Союзе и по настоящее время.
Гравиметры нового поколения CG-5 и CG-6 оснащены чувствительными емкостными индикаторами малых перемещений, что позволило упростить кварцевую систему, уменьшить ее размеры, сделать неастатизированной и значительно повысить точность измерений [5]. Кроме того, оснащение гравиметров блоками компьютерной обработки позволяет вводить вычисленные поправки в показания прибора в режиме реального времени, существенно снизив влияние помех и обеспечив точность измерений порядка 0,001 мГал. Автоматическое снятие показаний и непрерывная дискретизация данных минимизировали ошибки оператора
Гравиметр ГНУ-КВ был адаптирован для регистрации вариаций гравитационного поля с использованием видеокамеры в качестве ключевого элемента процесса цифровизации показаний. Это инновационное решение позволяет с высокой точностью фиксировать и детально анализировать вариации гравитационного поля, в том числе амплитудно-частотные характеристики (АЧХ) [3][9].
2.3. Процедура измерений
В рамках исследования был использован трехчасовой интервал наблюдения группой из четырех гравиметров: ГНУ-КВ, SCINTREX CG-5 (CG-350 и CG-351), и SCINTREX CG-6. Все временные ряды были приведены к единой системе отсчета с использованием единого масштабирования, обеспечив тем самым синхронизацию данных между различными гравиметрами Xnorm = [X – min(X)] / [max(X) – min(X)].
2.4. Обработка данных
Традиционные методы математического моделирования временных вариаций гравитационного поля сталкиваются с рядом ограничений, связанных с высокой сложностью учета множества факторов, влияющих на колебания земной поверхности. В связи с этим в данной работе предлагается безмодельный подход, основанный на использовании феноменологических моделей для подгонки экспериментальных данных. Такой подход позволяет эффективно описывать динамические свойства сложных систем даже при отсутствии точных аналитических выражений для всех влияющих процессов [7].
Для анализа вариаций гравитационного поля была применена комплексная методика, включающая спектрально-статистический анализ и преобразование Фурье. Известно, что дискретные значения случайной величины часто соответствуют процессам, близким к нормальному закону распределения [12].
Коэффициент корреляции Пирсона был использован для оценки степени линейной зависимости между временными рядами измерений различных гравиметров. Формула для расчета коэффициента корреляции представлена ниже:
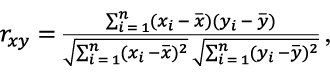 (1)
(1)
где rxy — коэффициент корреляции (или, иными словами, коэффициент корреляции Пирсона) между переменными x и y измеряет степень линейной зависимости между ними (от -1 до 1), x и y — наблюдаемые значения переменных, x и y — средние значения переменных x и y.
На рисунке 1 представлены результаты измерений (исходные кривые) вариаций гравитационного поля 4-х гравиметров. По оси ОХ — время, по оси ОУ отложены безразмерные и нормированные амплитуды.

Рис. 1. Результаты измерений (исходные кривые) вариаций гравитационного поля для всех 4-х гравиметров: а — ГНУ-КВ; б — CG-5-350; в — CG-5-351; г — CG-6
Fig. 1. Results of measurements (initial curves) of variations in the gravitational field for all 4 gravimeters: a — GNU-KV; б — CG-5-350; в — CG-5-351; г — CG-6
Низкие значения коэффициентов корреляции указывают на слабую линейную зависимость между временными рядами, что может быть связано с различиями конструктивных схем и технологий компенсации сползания ноль-пункта.
Для преодоления ограничений временного анализа была выполнена обработка сигналов в частотной области с использованием амплитудно-частотных характеристик (АЧХ). Этот подход позволяет сравнивать спектральное содержание сигналов и выявлять скрытые закономерности и взаимосвязи в частотной области.
2.5. Спектральный анализ
Для всех временных рядов были вычислены Фурье-спектры (рис. 2), соответствующие каждому гравиметру в той же последовательности, что и на рисунке 1. На этих графиках представлены только модули амплитуд, а фазовые характеристики всех приборов и анализ их зависимости являются предметом будущего отдельного исследования.
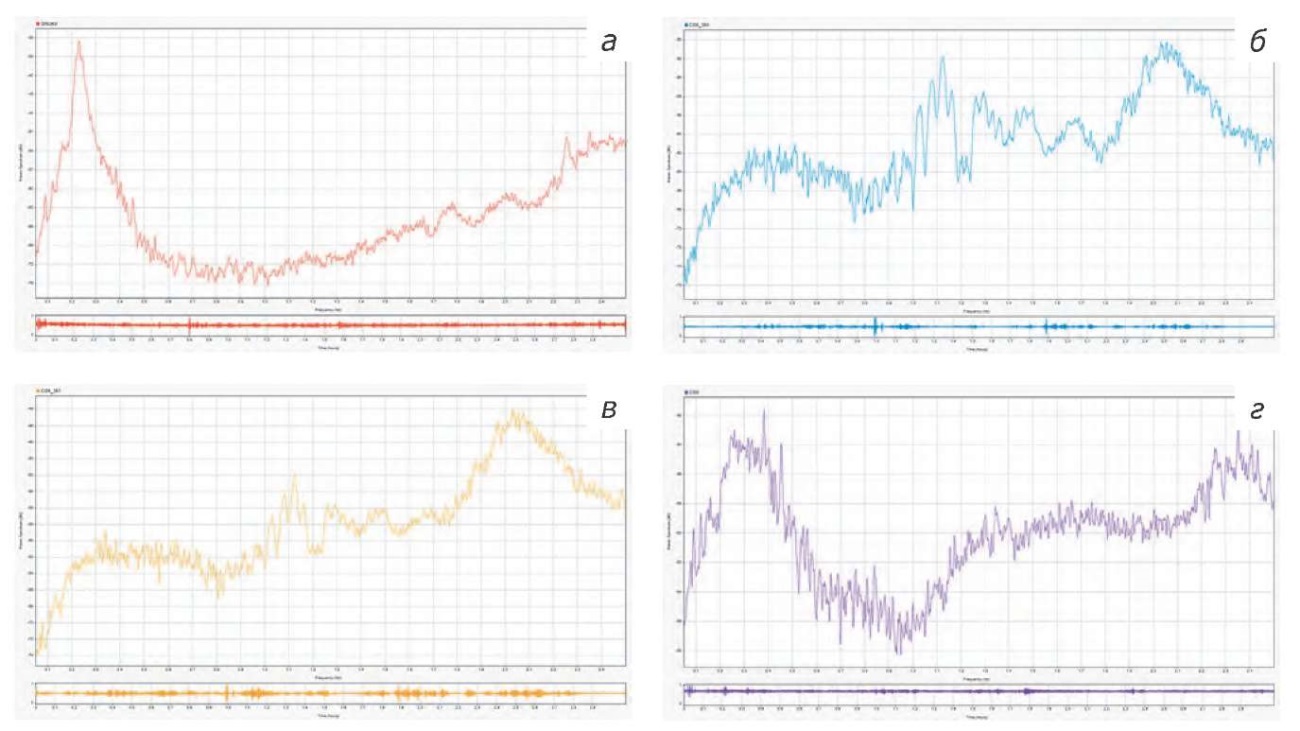
Рис. 2. Результаты анализа спектральных характеристик исходных данных
Fig. 2. Results of the analysis of spectral characteristics of the original data
CG-5 (CG-350 и CG-351) демонстрируют высокое совпадение АЧХ по амплитудным характеристикам, что объясняется их конструктивной идентичностью и одинаковыми заводскими механизмами регистрации (рис.2б и в).
В данной работе анализ АЧХ ограничивается только для пары приборов ГНУ-КВ и SCINTREX CG-6, так как SCINTREX CG-6 является базовым прибором при регистрации вариаций гравитационного поля на фундаментальном гравиметрическом пункте «Ледово». Из визуального анализа распределения АЧХ для пары приборов ГНУ-КВ и SCINTREX CG-6 наблюдается хорошее совпадение модулей амплитуд АЧХ по частотным характеристикам (рис. 3б). На этих графиках представлены только модули амплитуд, а фазовые характеристики всех приборов и анализ их зависимости являются предметом будущего отдельного исследования.
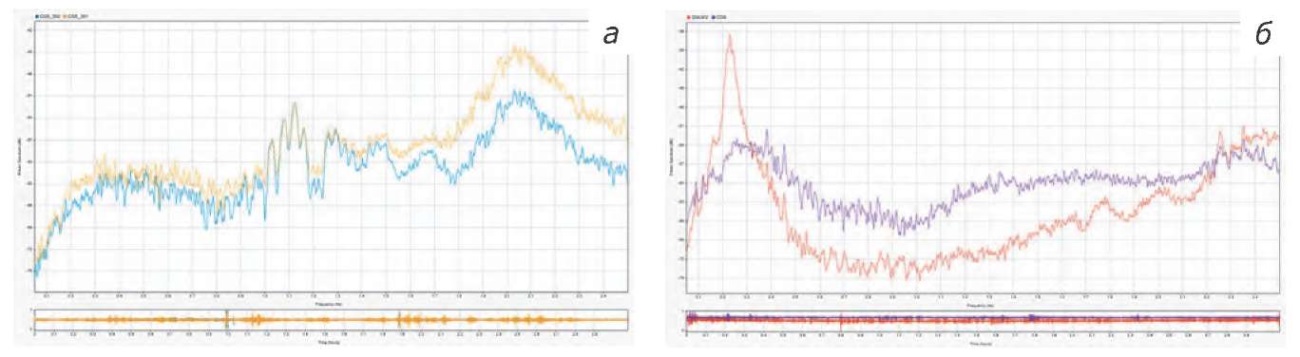
Рис. 3. Сравнение АЧХ гравиметров: а — сравнение SCINTREX CG-350 и CG-351; б — ГНУ-КВ и CG-5
Fig. 3. Comparison of the frequency response of gravimeters: a — comparison of SCINTREX CG-350 and CG-351; б — GNU-KV and CG-5
Таблица 1. Коэффициенты корреляции Пирсона между временными рядами гравиметров
Table 1. Pearson correlation coefficients between gravimeter time series
Пары гравиметров | Коэффициент корреляции (r) |
ГНУ-КВ и CG6 | 0,0285 |
ГНУ-КВ и CG5 350 | 0,0072 |
ГНУ-КВ и CG5 351 | 0,1010 |
CG5 350 и CG6 | -0,0011 |
CG5 351 и CG6 | 0,0138 |
Таблица 2. Корреляционные параметры для пары гравиметров ГНУ-КВ и SCINTREX CG-6
Table 2. Correlation parameters for a pair of gravimeters GNU-KV and SCINTREX CG-6
№ | Начало интервала, Гц | Окончание интервала, Гц | Внешняя корреляция | Корреляция Пирсона | Внутренняя корреляция P1 | Внутренняя корреляция Р2 |
1 | 0,05590 | 0,08258 | 0,33473 | 0,98049 | 0,94881 | 0,15364 |
2 | 0,08267 | 0,10935 | 0,32643 | 0,99127 | 0,85045 | 0,00000 |
3 | 0,10944 | 0,13612 | 0,38338 | 0,98470 | 0,93284 | 0,85085 |
4 | 0,13621 | 0,16290 | 0,58811 | 0,99259 | 0,93256 | 0,01125 |
5 | 0,16299 | 0,18967 | 0,37541 | 0,99579 | 0,68148 | 0,04431 |
6 | 0,18976 | 0,21644 | 1,19763 | 0,98571 | 0,94924 | 0,94979 |
7 | 0,21653 | 0,24321 | 1,28613 | 0,98712 | 0,76093 | 0,31125 |
8 | 0,24330 | 0,26998 | 1,23011 | 0,96287 | 0,17545 | 0,00674 |
9 | 0,27007 | 0,29676 | 0,44237 | 0,98776 | 0,78783 | 0,00000 |
10 | 0,29685 | 0,32353 | 0,27078 | 0,99391 | 0,93034 | 0,93034 |
11 | 0,32362 | 0,35030 | 0,22353 | 0,99557 | 0,36756 | 0,00000 |
12 | 0,35039 | 0,37707 | 0,16741 | 0,99742 | 0,91899 | 0,72916 |
13 | 0,37716 | 0,40385 | 0,24591 | 0,99913 | 0,90147 | 0,12485 |
14 | 0,40394 | 0,43062 | 0,29635 | 0,99941 | 0,94617 | 0,58750 |
15 | 0,43071 | 0,45739 | 0,37903 | 0,99260 | 0,91759 | 0,74302 |
16 | 0,45748 | 0,48416 | 0,45718 | 0,99950 | 0,97730 | 0,63309 |
17 | 0,48425 | 0,51094 | 0,25679 | 0,99607 | 0,82016 | 0,00000 |
18 | 0,51103 | 0,53771 | 0,41669 | 0,99171 | 0,80994 | 0,02425 |
При детальном рассмотрении распределения АЧХ (табл. 2) для пары ГНУ-КВ и SCINTREX CG-6 по отдельным участкам (дробная корреляция) выявлено хорошее совпадение как по амплитудным, так и по частотным характеристикам для отдельных интервалов частот.
Анализ таблицы 2 показывает, что корреляции, выделенные черным цветом, отражают различную степень близости сравниваемых случайных последовательностей, вычисленную по формулам (4), приведенным ниже. Наиболее близкими между собой являются пары 6 и 10, выделенные синим цветом.
2.6. Обобщенные корреляционные методы
В данной работе использовались как традиционная формула Пирсона (1), так и обобщенные корреляционные методы, позволяющие учитывать сложные зависимости между временными рядами. Они рассмотрены в недавней монографии [7]. В частности, были введены понятия внешних и внутренних корреляций, описываемые формулами (2) и (3) соответственно.
Формула (2). Внешняя корреляция
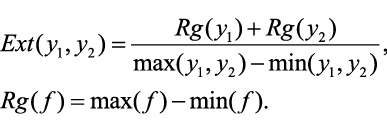 (2)
(2)
Формула (3). Внутренняя корреляция
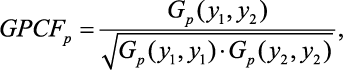
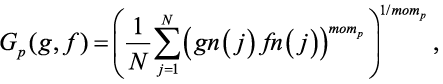 (3)
(3)

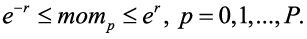
В главе 9 монографии [7] объясняется, что корреляции в современной математической статистике являются относительными. Помимо традиционного коэффициента корреляции Пирсона (1), существуют два основных типа корреляций: внешние и внутренние.
Формула (2) используется для определения пересечения двух случайных кривых. Если эти кривые пересекаются, то значение внешней корреляции Ext(y1,y2) будет находиться в диапазоне от 1 до 2. Если пересечений нет, то Ext(y1,y2) будет в диапазоне от 0 до 1.
Внутренние корреляции, показанные в последних двух столбцах таблицы 2, рассчитываются по более общей формуле (3). В этой формуле gn(j) и fn(j) — это две нормированные функции в диапазоне от 0 до 1. Диапазон моментов охватывает широкий интервал (e–r, er), и для их полного охвата достаточно выбрать r = 10.
Анализ обобщенной корреляционной функции дробных моментов (ОКФДМ) (3) показывает, что функция в диапазоне от 0 до 1 имеет две важные инвариантные точки (появляющиеся для всех сравниваемых функций): минимальную точку (М) и точку выхода на плато справа (Lm). Эти две точки позволяют определить значения корреляций на всей совокупности моментов в интервале (e-r, er). Эти значения обозначены как P1 и P2 и приведены в таблице 2. Они рассчитываются по формуле (4):
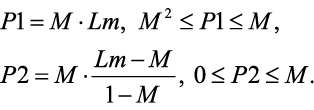 (4)
(4)
Из таблицы 2 видно, что коэффициент корреляции Пирсона дает завышенные значения корреляции, а параметры P1 и P2 — заниженные. Настоящие корреляции достигаются, когда внешняя корреляция Ext(y1,y2) превышает единицу, а внутренние корреляции P1 и P2 близки к минимальному значению M. Полное совпадение двух кривых происходит, когда Ext(y1,y2) = 2 и М = 1. Анализ этих параметров позволяет оценить степень корреляции сравниваемых кривых gn(j) и fn(j). Из таблицы 2 видно, что только пары 6 и 10 соответствуют этим требованиям.
2.7. Модели аппроксимации
Для понимания механизма влияния внешних процессов на вариации гравитационного поля необходимо найти математическую функцию, значения которой максимально приближены к экспериментальным гравиметрическим данным. Это достигается с помощью аппроксимации данных эмпирическими функциями. Аппроксимация позволяет изучать числовые характеристики и свойства объекта, сводя задачу к анализу более простых математических моделей. Процесс аппроксимации заключается в построении функции, которая наилучшим образом соответствует исходным данным с минимальной погрешностью.
2.8. Критерии выбора модели аппроксимации
Выбор модели аппроксимации определяется минимизацией ошибки на всем диапазоне исходных данных и максимизацией коэффициента детерминации R². Коэффициент детерминации R² измеряет, насколько хорошо модель объясняет вариации данных, и рассчитывается по следующей формуле:
R² = 1 – D[y] / D[y ↑ x], (5)
где D[y] — дисперсия зависимой переменной y, D[y ↑ x] — условная дисперсия y при заданных факторах x (дисперсия ошибки модели).
Таким образом, цель аппроксимации — построить математическую модель, максимально приближенную к «идеальной» модели, которая воспроизводит измеренные данные с минимальными ошибками и высокой достоверностью.
При выборе подходящей аппроксимирующей функции необходимо учитывать параметры, наиболее точно описывающие зависимость между изучаемыми величинами. Из нескольких подходящих вариантов выбирается та функция, которая обеспечивает максимальное значение R² и минимальную погрешность на всем диапазоне данных. Оценка качества моделей проводится на основе баланса между точностью аппроксимации и простотой вычислительной конструкции модели.
2.9. Рассмотренные модели аппроксимации
Для дальнейшего анализа были рассмотрены следующие модели аппроксимации исходных данных:
- Полиномиальные аппроксимации
- Фурье-аппроксимации
- Экспоненциальные аппроксимации
Представленные модели не охватывают все возможные варианты, но являются наиболее распространенными и простыми для аппроксимации наборов исходных данных.
Статистические показатели оценки моделей
Для оценки эффективности моделей использовались следующие статистические показатели:
- коэффициент детерминации (R²): измеряет степень достоверности аппроксимации между моделью и исходными данными;
- среднеквадратичная ошибка (RMSE): среднее квадратичное отклонение модели от исходных данных;
- сумма квадратов ошибок (SSE): общая сумма квадратичных отклонений модели от исходных данных.
Графическое представление результатов
Для удобного визуального сравнения качества моделей использовался кросс-плоттинг (диаграмма рассеяния). Кросс-плоттинг позволяет наглядно сравнить несколько измерений данных, отображая их на двух осях и более относительно друг друга. Обычно оси диаграммы линейны, но могут быть представлены в логарифмических и других (экспоненциальных, квадратичных и др.) шкалах.
Анализ кросс-плотов
Кросс-плоты использовались для визуальной оценки соответствия модели экспериментальным данным. На них откладывались экспериментальные значения по одной оси и значения модели по другой. Идеальная модель соответствует расположению точек вдоль линии под углом 45 градусов.
Анализ результатов:
Полиномиальная модель 2-й степени
- Качество модели (R² и RMSE):
- R² = 0,8197. Это говорит о хорошем соответствии модели исходным данным.
- Значение RMSE (среднеквадратичная ошибка) равно 0,091497.
- Значение SSE (сумма квадратов ошибок) составляет 229,7.
- Параметры модели: f(x) = 0,1719 + 4,0450x – 3,6688x².
- Графическое отображение (рис. 4а):
- График демонстрирует, что полиномиальная модель 2-й степени неплохо подстроилась под данные, особенно на начальном и среднем участках.
- Однако на концах графика видно, что модель отклоняется от фактических значений. Это может быть связано с тем, что данные имеют более сложное поведение, чем может описать полиномом 2-й степени.
Полиноминальная модель 3-й степени
- Качество модели (R² и RMSE):
- R² = 0,9440, что значительно выше по сравнению с предыдущей моделью 2-й степени. Это говорит о том, что модель 3-й степени лучше объясняет вариации в данных.
- Значение RMSE (среднеквадратичная ошибка) уменьшилось до 0,051017, что указывает на более низкий уровень ошибки по сравнению с полиномом 2-й степени.
- Значение SSE (сумма квадратов ошибок) также снизилось до 71,412, что свидетельствует о повышении качества аппроксимации.
- Параметры модели:
- Модель имеет вид: f(x) = 0,1501 + 5,2306x – 10,6823x² + 6,2094x³.
- Графическое отображение (рис. 4б):
- Модель 3-й степени лучше подстраивается под сложные нелинейные зависимости в данных и более точно повторяет тренды.
Полиноминальная модель 4-й степени
- Качество модели (R² и RMSE):
- R² = 0,8364, что ниже по сравнению с полиномиальной регрессией 3-й степени. Это говорит о том, что увеличение степени полинома привело к снижению качества модели.
- Значение RMSE (среднеквадратичная ошибка) равно 0,087156, что лучше по сравнению с полиномом 2-й степени, но хуже, чем у модели 3-й степени.
- Значение SSE (сумма квадратов ошибок) — 208,41, что указывает на некоторое улучшение в сравнении с моделью 2-й степени, но все еще хуже, чем у модели 3-й степени.
- Параметры модели:
- Модель имеет вид: f(x) = 0,1299 + 6,1593x – 18,3722x² + 23,1825x³ – 10,4337x⁴.
- Графическое отображение (рис. 4в):
- Модель 4-й степени демонстрирует хорошие результаты на начальном участке и лучше подстраивается под нелинейные зависимости на средней части графика. Однако на концах диапазона данные начинают отклоняться от аппроксимирующей кривой.
Анализ разных моделей Фурье
f(x) = a0 + a1 · cos(x · w) + bi · sin(x · w).
Частоты для моделей Фурье подбирались методом параметрической подгонки [10].
- Модель Фурье с 1 гармоникой: R² = 0,6086, RMSE = 0,13482.
Низкий R² и высокая ошибка указывают на то, что одной гармоники недостаточно для описания зависимости.
- Модель Фурье с 2 гармониками: R² = 0,7612, RMSE = 0,1053.
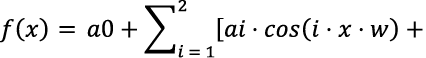
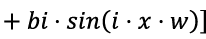
Увеличение числа гармоник улучшило качество модели.
- Модель Фурье с 3 гармониками: R² = 0,7721, RMSE = 0,10289
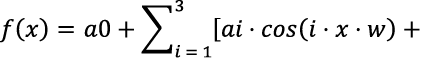
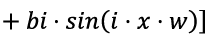
Дополнительная гармоника еще больше улучшила соответствие модели, снизив ошибку и увеличив R².
- Модель Фурье с 4 гармониками: R² = 0,7724, RMSE = 0,10282.
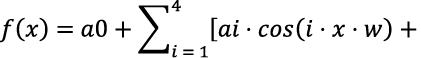
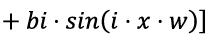
Увеличение числа гармоник до 4 уже не дало значительного улучшения по сравнению с моделью с 3 гармониками.
Оптимальная модель Фурье:
Модель Фурье с тремя гармониками показывает наилучшие результаты с R² = 0,7721 и относительно низким RMSE = 0,10289.
Анализ экспоненциальных моделей
- Экспоненциальная модель с 1 членом:
- Уравнение: f(x) = a · e(b · x)
- R² = 0,2405, RMSE = 0,1878
- Модель демонстрирует очень низкое значение коэффициента детерминации.
- Высокое значение ошибки (SSE = 967,75) указывает на то, что данная модель не подходит для описания набора данных.
- Экспоненциальная модель с 2 членами:
- Уравнение: f(x) = a · e(b · x) + c · e(d · x)
- R² = 0,7701, RMSE = 0,10331
- Модель значительно улучшает качество аппроксимации по сравнению с моделью с 1 членом.
- Значительно возросло значение R², что говорит о лучшем соответствии данных выбранной модели.
- Значение SSE снизилось до 292,84, что указывает на более точное описание данных.
- Увеличение в уравнении количества членов >2 приводит к значительным усложнениям технического характера вычислительной конструкции.
Экспоненциальная модель с 2 членами является более оптимальной, показывает гораздо лучшее соответствие данным (R² = 0,7701) и более низкую ошибку (RMSE = 0,10331). Модель с 1 членом слишком проста и не захватывает сложные зависимости в данных на данном интервале исследования.
На основании анализа всех моделей и различных типов аппроксимации можно сделать следующие выводы и рекомендации для нашего набора данных, где
- X — это спектр ГНУ-КВ,
- Y — это спектр CG-6.
Таблица 3. Результаты анализа всех моделей
Table 3. Results of analysis of all models
Тип модели | Уравнение | R² | RMSE | SSE | Вывод |
Полиномиальная | f(x) = p1 · x² + p2 · x + p3 | 0,8197 | 0,0915 | 229,7 | Хорошее соответствие, но не захватывает сложные колебания данных |
Полиномиальная | f(x) = p1 · x³ + p2 · x² + p3 · x + p4 | 0,9440 | 0,0510 | 71,4 | Лучшая аппроксимация среди полиномов. Оптимальная модель для наших данных |
Полиномиальная | f(x) = p1 · x⁴ + p2 · x³ + p3 · x² + p4 · x + p5 | 0,8364 | 0,0872 | 208,4 | Усложнение модели привело к ухудшению точности по сравнению с моделью 3-й степени |
Фурье | f(x) = a0 + a1 · cos(x · w) + bi · sin(x · w) | 0,6086 | 0,1348 | 498,7 | Недостаточно для описания данных с периодическими компонентами |
Фурье |
| 0,7612 | 0,1053 | 304,2 | Подходит для периодических данных, но точность ниже, чем у полинома 3-й степени |
Фурье |
| 0,7721 | 0,1029 | 290,4 | Лучшая Фурье-модель, но все еще уступает полиному 3-й степени |
Фурье |
| 0,7724 | 0,10282 | 290,01 | Увеличение числа гармоник не привело к значимому улучшению модели |
Экспоненциальная | f(x) = a · e(b · x) | 0,2405 | 0,1878 | 967,8 | Очень низкое соответствие. Не подходит для наших данных |
Экспоненциальная | f(x) = a · e(b · x) + c · e(d · x) | 0,7701 | 0,1033 | 292,8 | Хорошая аппроксимация для данных с экспоненциальными трендами |
Характеристики данных
- Данные имеют сложные и нелинейные зависимости, и на это указывает поведение кривых на рисунках 4—6.
- Спектры ГНУ-КВ и CG-6, судя по графикам, не имеют простой линейной или экспоненциальной зависимости. Сложные колебания и изменения трендов указывают на наличие как периодических, так и нелинейных компонентов, а также имеет место дробная корреляция. Также невозможно учесть все реальные геологические процессы.
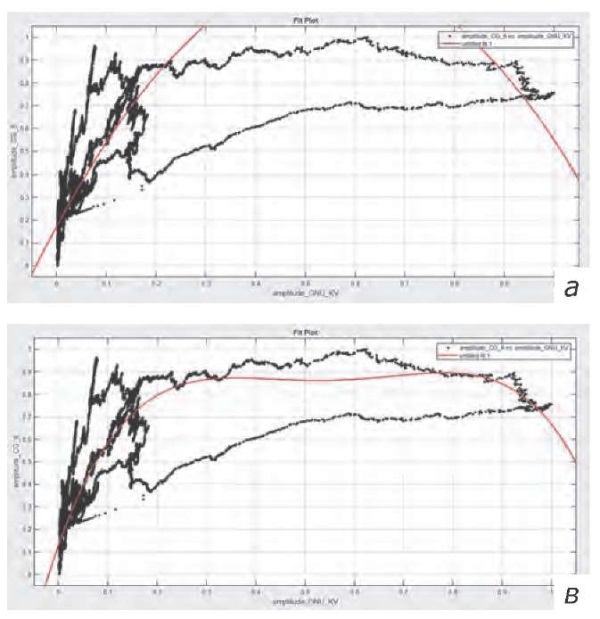
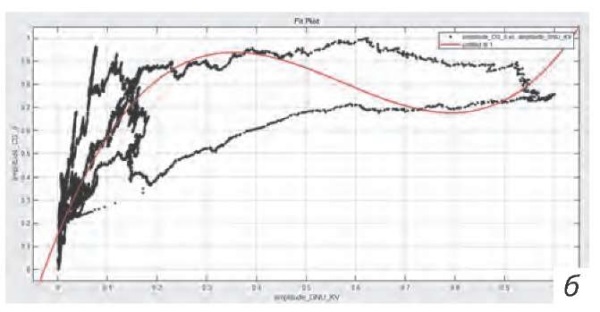
Рис. 4. Полиномиальные модели: а — 2-я степень с деталями расчетов; б — 3-я степень; в — 4-я степень
Fig. 4. Polynomial models: a — 2nd degree with calculation details; б — 3rd degree; в — 4th degree
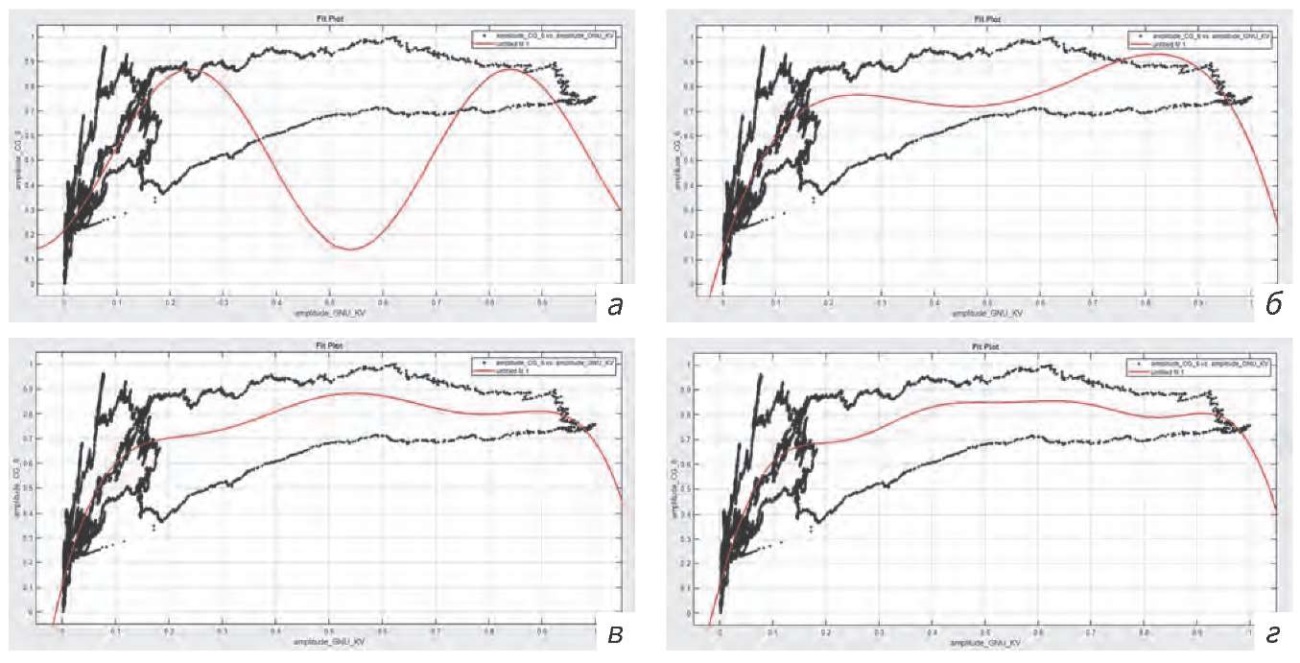
Рис. 5. Гармоники: а — 1; б — 2; в — 3; г — 4
Fig. 5. Harmonics: a —1; б — 2; в — 3; г — 4
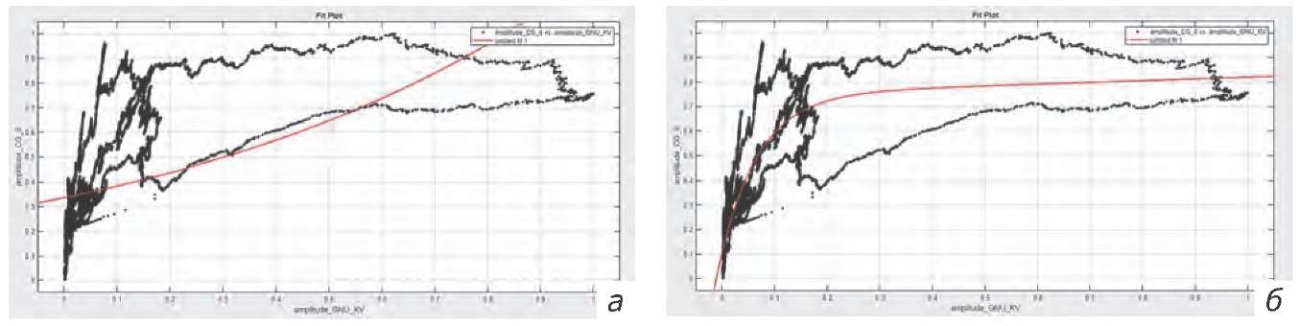
Рис. 6. Экспоненциальные модели. а — 1 член; б — 2 члена
Fig. 6. Exponential models. a — 1 part; б — 2 parts
Полиномиальные аппроксимации
- Полиномы 2-й и 3-й степени показали хорошее соответствие данным принятой модели.
- Полином 3-й степени продемонстрировал наилучшие результаты с R² ≈ 0,9440 и низким значением RMSE = 0,0510, что свидетельствует о хорошей подстройке к данным при умеренной сложности модели.
- Полином 4-й степени привел к ухудшению качества и возможному усложнению модели.
- Полином 3-й степени является оптимальным выбором среди полиномиальных моделей для наших данных.
Фурье-аппроксимации
- Модели Фурье использовались исходя из предположения о наличии периодической составляющей в регистрируемых данных:
- Фурье-модель с 3 гармониками показала наилучшие результаты (R² ≈ 0,7721), что указывает на наличие периодических компонентов в данных.
- Увеличение числа гармоник до 4 дало лишь минимальное улучшение и приводит только к усложнению модели.
- Фурье-модель с 3 гармониками достаточно хорошо описывает данные, учитывая их периодическую составляющую.
Экспоненциальные аппроксимации
- Экспоненциальные модели использовались для анализа экспоненциального роста или затухания:
- Модель с 1 членом имела низкий коэффициент корреляции и высокую ошибку.
- Экспоненциальная модель с 2 членами показала значительное улучшение (R² ≈ 0,7701) и снижение RMSE, что указывает на наличие экспоненциальных зависимостей в исследуемых данных.
- Экспоненциальная модель с увеличением количества членов > 2 уравнения приводит к значительным усложнениям технического характера вычислительной конструкции.
- Экспоненциальная модель с 2 членами является лучшим выбором для захвата экспоненциальных трендов, если они присутствуют в данных.
Полученные измерения ГНУ-КВ имеют достаточно высокую корреляцию с измерениями CG-6. Выявлена идентичность спектральных характеристик ГНУ-КВ и CG-6.
Если полином третьей степени достаточно хорошо описывает функцию на заданном интервале по критерию R², то использование четырех гармоник Фурье становится избыточным. Полином третьей степени способен описать функции с максимум двумя перегибами, что соответствует его аналитической структуре. С другой стороны, три гармоники Фурье могут создавать до шести перегибов, что излишне для описания функций, которые уже достаточно точно аппроксимируются этим полиномом. При этом полином третей степени требует меньше параметров (четыре коэффициента) по сравнению с тремя гармониками Фурье (шесть параметров: три амплитуды и три фазы). Это упрощает интерпретацию модели и значительно снижает вычислительную нагрузку. Таким образом, если полином обеспечивает достаточно высокое качество аппроксимации (R²≈ 1), то увеличение гармоник Фурье не добавляет значимой точности, а лишь усложняет модель.
Наилучшие результаты для данного интервала исследования показали полиномиальные модели 3-й степени. Фурье-модели также оказались полезны, особенно для учета периодических колебаний, однако полиномиальная модель 3-й степени обеспечивает несколько лучшее соотношение между точностью и простотой модели.
2.10. Метод ПОЛС
Помимо традиционных аппроксимаций, описанных выше, можно применить метод ПОЛС (процедура оптимального линейного сглаживания) [16].
Эта процедура весьма гибкая. Формула ПОЛС имеет вид:
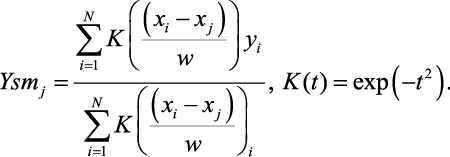 (6)
(6)
Здесь yj, Ysmj (j = 1, 2, … N) — соответственно, исходная и сглаженная функции, K(i,j) ядро сглаживания, выраженное через функцию Гаусса, а параметр w определяет окно сглаживания. Варьируя параметр w, мы можем получить различную степень сглаживания исходной функции yj, задавая коэффициент корреляции Пирсона (1) в интервале (0,95—0,99). Заметим, что в предельных случаях формула (5) приводит, соответственно, к среднему арифметическому (w >> 1) и когда (w → 0) Ysmj ≈ yj, отсутствию усреднения. Еще один существенный момент применения формулы (6) связан с тем фактом, что расчеты по ней линейны относительно сглаживаемой функции yj , что не приводит к дополнительным ошибкам обработки данных. Поэтому применение ПОЛС значительно приближает нас к построению модели, наиболее близкой к «идеальной» модели по минимуму относительной ошибки и максимальному значению величины коэффициента корреляции.
На рисунке 7 графики показывают результат применения ПОЛС к исходным данным, показанным ранее на рисунках 2 (слева и по центру) и 4. Отличие центрального рисунка (б) от рисунка слева (а) состоит в том, что на центральном рисунке оба спектра от гравиметров X (ГНУ-КВ) и Y (CG-6) приведены к единому масштабу. Величина окна сглаживания w = 0,05. Величина корреляции Пирсона между исходными данными и сглаженными спектрами лежит в интервале (0,98, 0,99). Наиболее интересен рисунок кросс-плоттинга, показанный справа (рис. 7). Этот рисунок ясно показывает, что на самом деле эта кривая многозначна и состоит из трех ветвей. Именно этим фактом объясняются не совсем удачные попытки аппроксимации традиционными функциями как полиномами, гармониками Фурье и экспонентами.
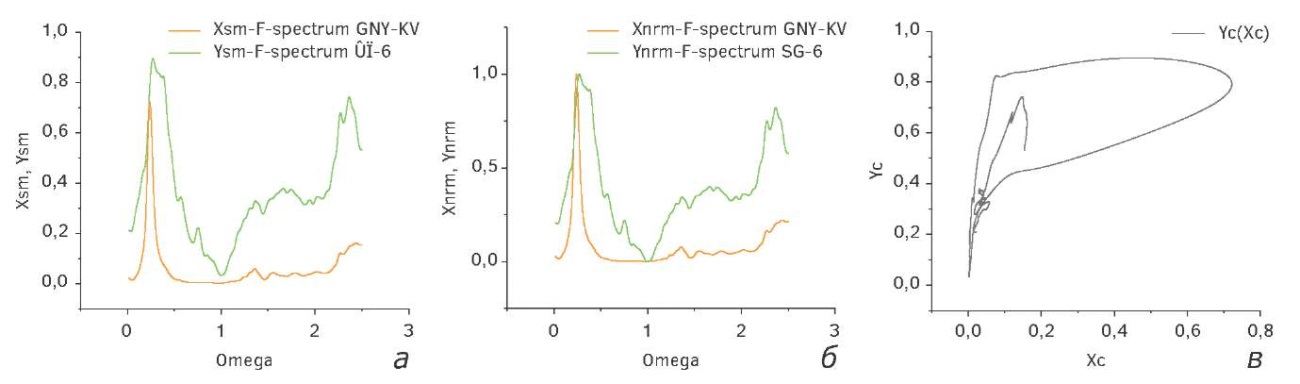
Рис. 7. Результаты применения ПОЛС к исходным данным
Fig. 7. Results of applying the POL to the initial data
Чтобы преодолеть этот существенный недостаток, можно упорядочить амплитуды (в порядке возрастания слева направо) исходных Фурье спектров и рассмотреть их упорядоченные структуры.
Если упорядочить амплитуды сглаженных Ф-спектров (рис. 8), то из рисунка (а), изображенного слева, получатся две упорядоченные кривые, изображенные на центральном рисунке. Кросс-плот этих кривых изображен на крайнем правом рисунке (в).
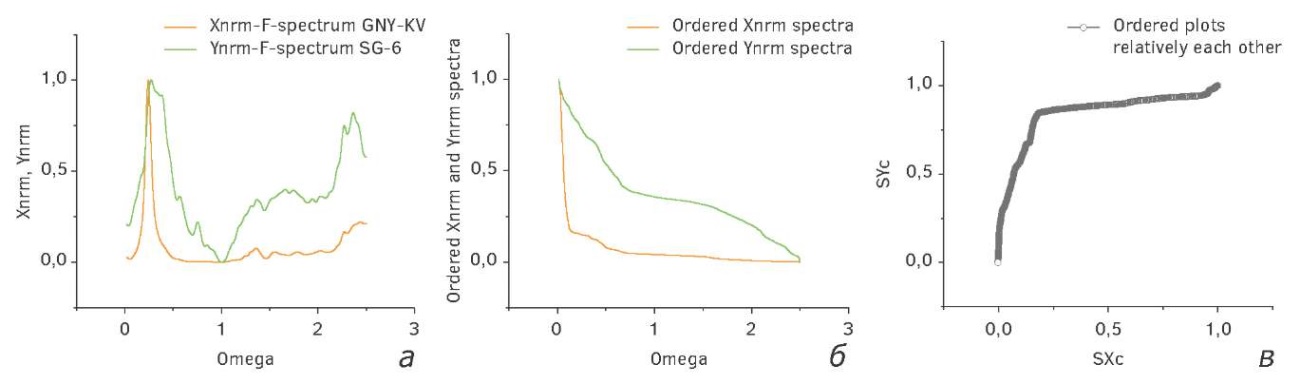
Рис. 8. Упорядоченные амплитуды сглаженных Ф-спектров
Fig. 8. Ordered amplitudes of smoothed F-spectra
Если сравнить рисунки (в), изображенные на рисунках 7 и 8, то можно заметить, что многозначность исчезает и остается крайняя верхняя ветвь, поддающаяся точному подгону. Подгон этой ветви осуществляется 2-экспоненциальной функцией вида:
Ysm = A0 + A1 exp(λ1 SXc) + A2 exp(λ2 SXc). (7)
Эта экспоненциальная функция содержит 5 подгоночных параметров (A0,1,2, λ1,2). Их значения таковы: A0 = 0,911, A1 = -0,807, A2 = 0,375 · 10⁻³; λ1 = -9,810, λ2 = 5,179.
График подгона этой функцией представлен на рисунке 9.
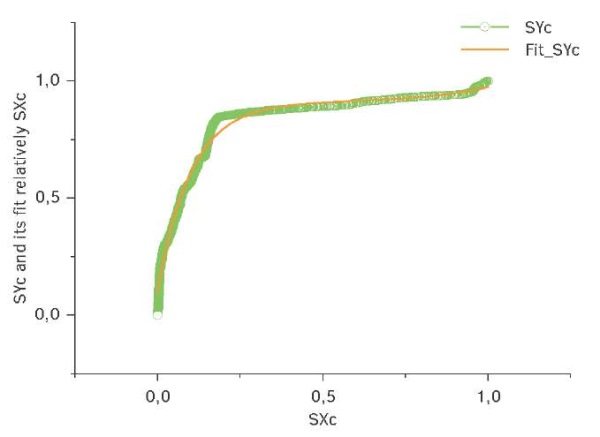
Рис. 9. Подгоночная кривая феноменологической модели
Fig. 9. Fitting curve of the phenomenological model
Подгоночная кривая, показанная оранжевой сплошной линией, подгоняет значительное число измеренных красных точек (N = 27 440) с относительной ошибкой меньше 1% (рис. 9). Именно эту подгоночную функцию можно будет использовать в качестве феноменологической модели для описания нестационарных вариаций гравитационного поля.
Общий вывод из анализа ряда математических моделей, рассмотренных выше по аппроксимации вариаций гравитационного поля, сводится к тому, что эта задача является достаточно сложной. Возможно, выбор модели должен учитывать, что конечный процесс, определяющий вариации гравитационного поля, состоит из смеси стационарных периодических процессов и случайных процессов неизвестной и неизученной природы.
Поэтому вариации гравитационного поля невозможно описать математически однозначно и аппроксимировать моделью только одного процесса. Имеет место сильное влияние недоучтенных и неизвестных случайных факторов процессов. Измерения, определяющие вариации гравитационного поля, являются, скорее всего, квазипериодическими. Но такая достаточно строго обоснованная с разных сторон математическая модель процесса, описывающая вариации гравитационного поля, в настоящее время отсутствует.
В работе [15] был предложен теоретический подход (подкрепленный также экспериментальными данными) для описания сложных моделей, связанных с квазипериодическими измерениями. Из этой теории следует важный вывод, связанный с тем, что каждый набор квазипериодических измерений может иметь две подгоночные функции: (а) связанную с предлагаемой моделью и (б) связанную с учетом влияния неконтролируемых факторов.
Общая модель таких квазипериодических измерений является случайной смесью известной предполагаемой модели и модели, учитывающей влияние случайных «гостевых» процессов (порожденных внешними случайными факторами). Такую ситуацию можно определить как проверяемый принцип частичной корреляции (ППЧК) [15]. Таким образом, на основе этого принципа можно будет получить общую математическую модель (определяемую как промежуточная модель — ПМ). Поскольку эксперимент, проводимый с этим набором переменных, является однофакторным, предполагается, что другие контролируемые переменные, влияющие на функцию отклика, не изменяются (или их влияние является малым) в некотором диапазоне их значений во время однофакторного эксперимента. В результате можно получить общую подгоночную функцию, представленную в упрощенной форме в виде отрезка ряда Прони [16] — которая содержит достаточно малое число подгоночных параметров.
Только увеличение числа повторных измерений позволит уменьшить влияние случайных ошибок и неконтролируемых факторов, приближая потенциального исследователя к правильному пониманию построения модели реального процесса. Именно в рамках такой модели, основанной на ППЧК, можно будет найти приемлемую для практических нужд модель, описывающую временные вариации гравитационного поля. Другими словами, чтобы повысить достоверность данных, нам потребуется работать с еще большим количеством экспериментов, которые должны быть, по крайней мере, квазивоспроизводимыми для выбранного промежутка времени их измерений. Разумеется, такое исследование выходит за рамки этой работы (лишь указывающей на невозможность описания вариаций гравитационного поля в рамках общепринятых подходов) и будет являться уже предметом дальнейшего исследования.
Выводы
- Высокая корреляция между гравиметрами ГНУ-КВ и CG-6: анализ измерений показал высокую степень корреляции между данными гравиметров ГНУ-КВ и CG-6, а также выявлены идентичные спектральные характеристики этих приборов. Это подтверждает надежность приборов и точность регистрации временных вариаций гравитационного поля.
- Сложность математического описания вариаций гравитационного поля: однозначное математическое моделирование вариаций гравитационного поля в рамках одной модели невозможно из-за значительного влияния недоучтенных геодинамических процессов и других случайных факторов.
- Предложен новый подход к моделированию вариаций гравитационного поля: вариации гравитационного поля рассматриваются как случайная смесь известной базовой модели и модели, учитывающей влияние случайных «гостевых» процессов, вызванных внешними случайными факторами.
- Эффективность применения процедуры оптимального линейного сглаживания (ПОЛС): использование ПОЛС позволяет создать модель, близкую к «идеальной», минимизируя относительную ошибку аппроксимации и максимизируя коэффициент корреляции Пирсона.
- Необходимость увеличения числа измерений: для более точного построения модели реального процесса и снижения влияния случайных ошибок и неконтролируемых факторов требуется увеличить количество повторных измерений и расширить интервал наблюдений. Это позволит получить более достоверные данные и повысить качество интерпретаций, приближая модель к комплексному описанию временных вариаций гравитационного поля.
ВКЛАД АВТОРОВ / AUTHOR CONTRIBUTIONS
Нигматуллин Р.Р. — разработал математический аппарат, внес вклад в идею и концепцию статьи, присоединился к подготовке текста статьи, окончательно утвердил публикуемую версию и согласен принять на себя ответственность за все аспекты работы.
Белов А.П. — внес вклад в разработку постановку задач, принял участие в постановке задач, формулировании идей. Принял участие в разработке концепции проведения эксперимента. Присоединился к подготовке текста статьи, окончательно утвердил публикуемую версию и согласен принять на себя ответственность за все аспекты работы. Оказал помощь в формировании выводов.
Ерохин А.М. — внес основной вклад в разработку концепции статьи, сформулировал идеи и постановку задач, предложил способ решения поставленных задач, раскрыл причинно-следственные связи. Провел сбор, обработку и анализ исходных данных. Провел математические вычисления и разработал программный код для их проведения, провел моделирование, подготовил иллюстрации. Описал и сформулировал выводы. Присоединился к подготовке текста статьи и окончательно утвердил публикуемую версию и согласен принять на себя ответственность за все аспекты работы.
Мухаметзянов А.Р. — провел оформление статьи, оказал помощь в сборе первичных материалов, помог организовать и провести эксперимент с технической стороны, участвовал в статистической обработке данных. Окончательно утвердил публикуемую версию и согласен принять на себя ответственность за все аспекты работы.
Конешов В.Н. — внес большой вклад в разработку концепции статьи, принял участие в постановке задач, формулировании идей. Оказал методологическую помощь в проведении сбора, обработки и анализа исходных данных. Принял участие в обсуждении результатов, оказал помощь в интерпретации полученных расчетов. Оказал руководящую и методологическую помощь в организации и проведении эксперимента, обеспечил лабораторию для проведения исследования. Присоединился к подготовке текста статьи, окончательно утвердил публикуемую версию и согласен принять на себя ответственность за все аспекты работы.
Дробышев М.Н. — принял участие в обсуждении задач, идей и концепции статьи. Оказал методическую помощь для сбора первичных данных, оказал техническую помощь в проведении эксперимента. Присоединился к подготовке текста статьи, окончательно утвердил публикуемую версию и согласен принять на себя ответственность за все аспекты работы.
Raoul R. Nigmatullin — Developed the mathematical framework, contributed to the idea and concept of the article, participated in preparing the manuscript, approved the final version to be published, and agrees to be accountable for all aspects of the work.
Alexey P. Belov — Contributed to the development and formulation of the research tasks and ideas, participated in designing the experiment, joined the preparation of the manuscript, approved the final version to be published, agrees to be accountable for all aspects of the work, and assisted in formulating the conclusions.
Alexandr M. Erokhin — made the primary contribution to developing the article’s concept, formulated the ideas and research tasks, proposed solutions and elucidated causal relationships; collected, processed and analysed the initial data; performed the mathematical calculations and wrote the corresponding software code; carried out the simulations and prepared the illustrations; drafted and formulated the conclusions; participated in preparing the manuscript, approved the final version to be published, and agrees to be accountable for all aspects of the work.
Amir R. Mukhametzyanov — handled the formatting of the article, assisted in collecting the initial materials, helped organise and conduct the experiment from the technical side, participated in the statistical processing of the data, approved the final version to be published, and agrees to be accountable for all aspects of the work.
Vyacheslav N. Koneshov — made a major contribution to developing the article’s concept, participated in formulating the research tasks and ideas; provided methodological assistance in collecting, processing and analysing the initial data; took part in discussing the results and helped interpret the calculations obtained; provided leading methodological support in organising and conducting the experiment and furnished the laboratory facilities for the study; participated in preparing the manuscript, approved the final version to be published, and agrees to be accountable for all aspects of the work.
Mikhail N. Drobyshev — participated in discussing the research tasks, ideas and concept of the article; provided methodological assistance in collecting the primary data and technical assistance during the experiment; participated in preparing the manuscript, approved the final version to be published, and agrees to be accountable for all aspects of the work.
Список литературы
1. Абрамов Д.В., Дорожков В.В., Конешов В.Н. Особенности построения и использования наземного сейсмогравиметрического комплекса. Сейсмические приборы. 2010. Т. 46, № 4. С. 5—13.
2. Абрамов Д.В., Дробышев М.Н., Конешов В.Н. Оценка влияния сейсмических и метеорологических факторов на точность измерений относительным гравиметром. Физика Земли. 2013. № 4. С. 105—110.
3. Белов А.П., Лобанов А.М., Ерохин А.М. Опыт амплитудно-частотной оценки колебания грунтов в диапазоне 0,05—0,5 Гц с использованием чувствительного элемента гравиметра ГНУ-КВ. Известия высших учебных заведений. Геология и разведка. 2023. № 65(2). С. 67—73. https://doi.org/10.32454/0016-7762-2023-65-2-67-73
4. Белов А.П., Лобанов А.М., Утесинов В.Н., Ерохин А.М., Венедиктов К.В. Статистический анализ функции распределения колебаний индикатора кварцевого гравиметра. Материалы 50-й юбилейной сессии Международного семинара им. Д.Г. Успенского — В.Н. Страхова «Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей». 2024. С. 38—41.
5. Гравиметры относительные СG-6 Autograv. All-Pribors.ru Измерительное оборудование]. URL: https://all-pribors.ru/opisanie/77100-19-sg-6-autograv#c3-texniceskie-xarakteristiki (дата обращения: 20.12.2024).
6. Дробышев М.Н., Конешов В.Н. Оценка предельной точности гравиметра CG-5 Autograv. Сейсмические приборы. 2013. Т. 49. № 2. С. 39—43.
7. Евдокимов Ю.К., Нигматуллин Р.Р., Денисов Е.С. Распределенные измерительные среды и системы. Фрактальная обработка сигналов. Фрактальная радиоэлектроника: в 2 тт. М.: Физматлит, 2024. 447 с.
8. Конешов В.Н., Дробышев Н.В., Сермягин Р.А., Разинькова Е.П. Результаты оценки абсолютных гравиметрических измерений на фундаментальном гравиметрическом пункте «Ледово» и гравиметрической сети России первого класса. Физика Земли. 2023. № 6. С. 199—206. https://doi.org/10.31857/S0002333723060091
9. Лобанов А.М., Белов А.П., Ерохин А.М., Венедиктов К.В. Алгоритм распознавания видеофайла для оцифровки колебаний аналогового индикатора на примере кварцевого гравиметра ГНУКВ. Известия высших учебных заведений. Геология и разведка. 2024. № 66(1). С. 128—134. https://doi.org/10.32454/0016-7762-2024-66-1-128-134
10. Метод параметрической подгонки (MATLAB). MathWorks. URL: https://www.mathworks.com/help/curvefit/fit.html (дата обращения: 20.12.2024).
11. Рикитаке Т. Предсказание землетрясений. М.: Мир, 1979. 388 с.
12. Торге В. Гравиметрия. М.: Мир, 1999. 428 с.
13. Чечкин С.А. Основы геофизики. Л.: Гидрометеоиздат, 1990. ISBN: 5-286-00436-9.
14. Юзефович А.П., Огородова Л.В. Гравиметрия. М.: Недра, 1980.
15. Nigmatullin R.R., Osokin S.I., Baleanu D., Al-Amri S., Azam A., Memic A. The first observation of memory effects in the infrared (FT-IR) measurements: do successive measurements remember each other? PLoS ONE. Open Access journal. 2014. April 9. No. 4. e94305.
16. Nigmatullin R.R., Litvinov A.A., Osokin S.I. Quasi-Reproducible Experiments: Universal Fitting Function for quantitative Description of Complex Systems Data. Lobachevskii Journal of Mathematics. 2024. Vol. 45. No. 8. P. 3956—3971.
17. Müller J., et al. A land uplift model in Fennoscandia combining GRACE and absolute gravimetry data. Physics and Chemistry of the Earth. 2012. Vol. 53. P. 54—60.
Об авторах
Р. Р. НигматуллинРоссия
Нигматуллин Равиль Рашидович — доктор физико-математических наук, профессор КНИТУ-КАИ.
10, ул. К. Маркса, Казань, 420111
Конфликт интересов:
Нет
А. П. Белов
Россия
Белов Алексей Павлович — кандидат геолого-минералогических наук, доцент.
23, ул. Миклухо-Маклая, Москва 117997
тел.: +7 (495) 255-15-10, доб. 21-52
Конфликт интересов:
Нет
А. М. Ерохин
Россия
Ерохин Александр Михайлович — заместитель начальника управления ИТ по научно-исследовательской работе.
4, корп. 2, Макарова ул., Тверь 170002
тел.: + 7 (915) 724-82-76
Конфликт интересов:
Нет
А. Р. Мухаметзянов
Россия
Мухаметзянов Амир Рустемович — аспирант.
23, ул. Миклухо-Маклая, Москва 117997
Конфликт интересов:
Нет
В. Н. Конешов
Россия
Конешов Вячеслав Николаевич — доктор технических наук, профессор, руководитель научного направления «Потенциальные поля» ИФЗ РАН.
10, стр. 1, ул. Большая Грузинская, Москва 123242
Конфликт интересов:
Нет
М. Н. Дробышев
Россия
Дробышев Михаил Николаевич — кандидат технических наук, ведущий научный сотрудник ИФЗ РАН.
10, стр. 1, ул. Большая Грузинская, Москва 123242
Конфликт интересов:
Нет
Рецензия
Для цитирования:
Нигматуллин Р.Р., Белов А.П., Ерохин А.М., Мухаметзянов А.Р., Конешов В.Н., Дробышев М.Н. Построение и анализ некоторых математических моделей, связанных с временными вариациями гравитационного поля. Proceedings of Higher Educational Establishments: Geology and Exploration. 2025;67(2):76-94. https://doi.org/10.32454/0016-7762-2025-67-2-76-94. EDN: JSULIZ
For citation:
Nigmatullin R.R., Belov A.P., Erokhin A.M., Mukhametzyanov A.R., Koneshov V.N., Drobyshev M.N. Construction and analysis of mathematical models describing temporal variations of earth’s gravity field. Proceedings of higher educational establishments. Geology and Exploration. 2025;67(2):76-94. (In Russ.) https://doi.org/10.32454/0016-7762-2025-67-2-76-94. EDN: JSULIZ